SOMMAIRE

Introduction

I) Applications fractales dans la nature

A) Côtes littorales bretonnes

B) Chou-fleur

C) La fougère

D) Déchirure de sac plastique

II) La fractale, une forme mathématique

A) Courbes fractales, construction d’une fractale

B) Ensemble de Mandelbrot

III) Propriétés fractales

A) Autosimilarité

B) Dimension fractale

C) Fractale et théorie du chaos, (l’effet papillon)

Conclusion

Lexique

Bibliographie

Introduction :

Jusqu’au siècle dernier, les mathématiciens n’étudiaient que les formes parfaites comme les triangles et les cercles, c’est-à-dire la géométrie euclidienne. Des formes aussi régulières existent-elles dans la nature ? - pensons aux dentelures d’un littoral ou aux reliefs déchiquetés d’une montagne. Contrairement au cercle, qui devient de plus en plus lisse et net lorsque nous l’agrandissons, la montagne reste tout aussi déchiquetée au fur et à mesure dont nous nous en rapprochons, parce que nous en distinguons de plus en plus les détails. Jusque vers les années 1970, ces formes irrégulières étaient difficilement étudiées et peu comprises, elles étaient considérées comme des « curiosités mathématiques ». Enfin, en 1975, le mathématicien français Benoit Mandelbrot donna un nom à ces formes indéfiniment irrégulières dans l’un de ses ouvrages: il forgea le néologisme « fractal » et en fit l’objet d’une nouvelle discipline : la géométrie fractale.

Le mot « fractal » est formé à partir de l’adjectif latin « fractus » qui signifie « brisé », « irrégulier ». Ce mot a été créé pour désigner un type d’objets qui se distinguent des formes géométriques comme la droite ou le cercle par leur irrégularité. Les fractales sont des objets mathématiques comme le sont les nombres entiers ou les quadrilatères ; ce sont des figures géométriques de structure complexe qui se répètent à l’infini à l’intérieur d’elles-mêmes, à des échelles très petites ou très grandes. Prenons pour exemple les poupées gigognes, ou poupées russes : c’est une figurine creuse en bois qui s'ouvre en deux horizontalement, révélant ainsi à l'intérieur une figurine similaire mais de taille plus petite. Cette seconde figurine renferme elle-même une autre figurine, et ainsi de suite. Généralement, les formes géométriques simples et classiques perdent leur forme primaire quand elles sont agrandies, c’est-à-dire que la partie agrandie devient plus lisse et sans détails. Or les objets fractals comportent toujours des irrégularités et les mêmes détails quelques soit l’agrandissement effectué.

Les fractales peuvent êtres classés en trois catégories :

- Les fractales aléatoires : elles ne sont pas contrôlées par des mécanismes ou des formules. Ce sont par exemple les paysages fractals, des fractales dites naturelles, soit tout ce que l’on peut trouver de naturel qui possède une structure fractale. Les fractales aléatoires sont les plus utilisées car elles correspondent à la plupart des phénomènes irréguliers, des reliefs et peuvent êtres applicables dans plusieurs disciplines.

- Les systèmes de fonctions itérés ou IFS (Iterated Function System) ont une structure compliquée mais sont générées par une théorie développée par John Hutchinson en 1981, utilisée dans le cadre de la géométrie fractale par Michael Barnsley. Les fractales IFS présentent donc la propriété d’autosimilarité, que nous expliquerons dans la partie de notre TPE concernant les propriétés fractales.

- Enfin, les fractales sont construites par récurrence, pour chaque point dans un espace. Ce sont des itérations, c’est-à-dire des répétitions de polynômes complexes en eux-mêmes comme l’ensemble de Mandelbrot que nous présenterons par la suite.

Nous commencerons par de nombreux exemples et applications fractales que nous pouvons retrouver dans la nature et notre environnement. Dans une deuxième partie, nous aborderons les fractales comme une forme mathématique. Puis, pour finir, nous étudierons les propriétés des fractales.

I. Fractales dans la nature

Les fractales sont à la base d’un nouveau système de géométrie permettant de représenter des objets très irréguliers tels que les reliefs montagneux, les amas galactiques ou les côtes rocheuses très découpées. Les choux-fleurs, les arbres, les nuages, les éclairs électriques, les montagnes, les poumons, les vaisseaux sanguins : ce sont tous des fractales naturelles. Ces dernières sont toutes des éléments et des phénomènes de la nature qui présentent des propriétés fractales. Cette catégorie regroupe donc les fractales qui se rapprochent le plus de notre quotidien. Mais ces objets naturels ne sont pas de vraies fractales, puisque leur complexité n'est pas infinie. La complexité s'arrête au niveau de l'atome, et non au niveau de l'infiniment petit. De même, elle ne s'étend pas dans l'infiniment grand.

Dans cette partie, nous allons vous présenter, les côtes bretonnes, le chou-fleur, la fougère et enfin, un exemple un peu moins naturel, le sac plastique.

A) Côtes littorales bretonnes

Les objets fractals ainsi définis ont des caractéristiques spécifiques assez étonnantes qui vont à l'encontre du sens commun.

Prenons un exemple : à votre avis quel est la longueur de la côte de Bretagne, entre Nantes et Le Havre ? Les dictionnaires et les atlas géographiques avancent des valeurs très différentes. Serait-ce parce que personne n'a vraiment mesuré cette distance ?

Si nous devons mesurer une longueur (une droite) de 1 m avec une règle de 20 cm, cette règle sera contenue 5 fois dans la longueur à mesurer. Si nous utilisons une règle de 10 cm, elle sera contenue 10 fois ; si elle fait 5 cm, elle sera contenue 20 fois. Supposons maintenant que la ligne à mesurer est plus ou moins courbe. En faisant le même procédé avec une règle de 20 cm, nous ne pourrons pas suivre exactement la courbure de la ligne et nous sous-estimerons sa longueur en comptant le nombre entier de fois que nous appliquons la règle sur la ligne. Avec une règle de 10 cm le résultat se rapprochera de la taille de la courbe. Plus la règle utilisée sera courte, mieux nous pourrons suivre le contour de la courbe, et plus le résultat sera précis.

ligne.gif (6591 octets) En termes plus mathématiques, le résultat converge vers la longueur exacte de la ligne lorsque la règle atteint une dimension négligeable par rapport à la courbure de la ligne.

Au sens de Mandelbrot dont nous parlerons aux § 2, les longueurs de la côte est infinie : si nous utilisons un segment infiniment petit, la longueur de cette côte devient infiniment longue !

Mandelbrot imagine, pour pouvoir décrire cette longueur infinie, la notion de dimension fractale. Pour Mandelbrot, le contour de la côte de Bretagne a une dimension probablement située entre 1 et 1,5. Plus ce contour est replié, plus il "occupe de la place sur les plans", et donc plus il tend à remplir la deuxième dimension. Avec les objets mathématiques bien définis, on peut calculer précisément cette dimension fractale. Pour avoir une longueur plus précise de la côte, il suffirait donc d’avoir une carte plus précise et plus grande.

$http://www.jutier.net/images/frac5.gif$

Nous allons maintenant nous intéresser à un légume que vous connaissez bien: le chou-fleur, aussi appelé asparagus major.

B) Chou-fleur

Le chou-fleur a une forme très complexe. Il ressemble à une section de sphère entourée de feuilles. Si on regarde de plus près la surface du chou-fleur, nous constatons que celle-ci est constituée de cônes qui se juxtaposent de manière enroulée en spirale, formant ainsi des volutes qui constituent elles-mêmes des cônes similaires aux premiers, mais d'échelle plus petite. Si nous ouvrons le chou-fleur en le cassant, nous observons une structure en branches principales qui se séparent en branches plus petites. La première division se produit sur la branche principale d'origine, et peut donner de 3 à 8 branches secondaires. Cette division se reproduit de la même façon à chaque étage avec régularité. A vu d'œil, nous pouvons distinguer entre 5 et 8 étages de divisions entre la branche d'origine et la surface du chou-fleur. A chaque étage, les subdivisions sont proportionnellement similaires. Pour cette expérience nous avons supposé qu'un chou-fleur, était composé d'une imbrication de choux-fleurs plus petits qui ont à peu près la même taille et la même forme. Ainsi nous n'avons pas pris en compte que ces "réductions" de chou-fleur étaient de forme irrégulière. Donc nous n’avons pu que remarquer l’autosimilarité, qui indique qu’un même motif est répété indéfiniment à des échelles de plus en plus petite et qui est une propriété des fractales que nous étudierons au § 3, sans démonstration.

Nous pouvons en conclure que, dans la nature, nous trouvons des objets qui représentent les caractéristiques mathématiques d’une courbe connue sous le nom de flocon de Von Koch que nous étudierons au § 2 : une répétition à toutes les échelles d'un motif similaire. Sur ce principe de subdivision et de répétition, nous pouvons énumérer une multitude de formes qui ressemblent à des objets naturels. Ces procédés sont souvent utilisés pour créer des décors en images de synthèse comme des paysages imaginaires frappants de réalisme, ou même des textures qui imitent les tissus et la pierre.

C) La fougère

Un mathématicien s'est intéressé de près aux objets de la nature, et a montré que l’on peut en fait générer toute forme, aussi complexe soit-elle, en utilisant un ensemble de fonctions simples itérées un grand nombre de fois.

La fougère ici est un autre exemple de forme fractale. Ce sont en particulier les feuilles ou frondes de la plante qui présentent cette particularité d’auto similarité. En effet la structure de la fougère se répète à plusieurs niveaux, à chaque étape on retrouve la même organisation, celle globale de la feuille

Mathématiquement, en utilisant un ensemble de fonctions simples itérées un grand nombre de fois, on peut obtenir des images de fougères très réalistes. Selon ce principe, on peut simuler la croissance de nombreux végétaux ce qui donne des images difficiles à distinguer de véritables photographies.

Fougère simulée par une fractale

Voyons maintenant l’exemple du sac plastique :

D) Déchirure de sac plastique

La bordure des feuilles de certaines plantes comme les lichens, les orchidées ou les laitues arborent des ondulations aussi belles que complexes qui intriguent les scientifiques. Elles sont dites « fractales », c'est-à-dire qu’elles présentent des similarités quelle que soit l'échelle à laquelle on les regarde. Chaque ondulation est constituée d'autres ondulations similaires trois à cinq fois plus petites, et ainsi de suite, parfois jusqu'à la cinquième génération. Dans une étude publiée dans Europhysics news en septembre 2004, des chercheurs ont pu expliquer puis simuler numériquement l'apparition de ces mêmes formes lorsque l'on déchire un film plastique, comme, par exemple, le sac plastique de supermarché. « L'origine de ces ondulations est la même pour le plastique déchiré et certaines feuilles en croissance, expliquent les chercheurs. Il s'agit d'un excès de longueur à leur périphérie qui doit être compensé ». En effet, lorsque le film plastique est déchiré, la zone proche des bords ainsi créés est étirée de manière irréversible, elle ne retrouvera plus sa forme initiale. Dans les deux cas de figure, la partie allongée doit se raccorder avec le reste de la surface. C'est pourquoi elle se déforme en adoptant la forme qui lui coûte le moins d'énergie. Les chercheurs ont donc calculé la solution la plus économique pour le film plastique en espérant ainsi retrouver les formes fractales. Or il est plus facile de courber une feuille que de l'étirer et ceci signifie que la première déformation coûte beaucoup moins d'énergie que la deuxième. La feuille va donc d'abord chercher à se courber de façon à minimiser l’énergie à dépenser. Cela expliquerait des ondulations simples mais pas nécessairement l'aspect fractal. Or, les chercheurs ont calculé que, pour minimiser cette énergie coûteuse due à l'élongation, la surface déformée doit acquérir, en chacun de ses points, une forme connue des mathématiciens, celle d'une selle de cheval, répliquée à toutes les échelles. C'est exactement ce qui donne le caractère fractal aux ondulations observées sur les plantes et les sacs plastique. Ces recherches, à l’intersection entre les voies de la physique et de la biologie, profitent aux deux disciplines en faisant émerger à la fois de nouveaux problèmes et des méthodes de résolution innovantes. Nous pouvons même jusqu’à aller penser que le sac plastique copie les plantes, donc la nature et ainsi le comportement fractal de celle-ci.

Déchirure d’un sac plastique

Notre environnement est donc constitué de nombreuses formes irrégulières présentant des propriétés fractales.

II. La fractale, une forme mathématique

Dans ce paragraphe, nous abordons l’aspect mathématique des fractales.

A) Courbes fractales, construction d’une fractale

Les objets fractals récurrents se définissent comme des structures obtenues par la répétition d’un calcul géométrique (ou algorithme), sur une figure. Pour construire des objets fractals, nous commençons avec un objet graphique quelconque (ligne, triangle, carré, cube, etc.) et nous définissons une opération, ou une série d’opérations, qui ajouteront un élément de complexité à l’objet initial. Les transformations choisies à l’objet de départ doivent êtres ensuite appliqués indéfiniment.

Les courbes fractales sont les fractales les plus simples à représenter. Elles sont obtenues grâce à une construction géométrique :

La plus connue des courbes de ce genre est la courbe de Von Koch appelée habituellement « flocon de neige de Von Koch ». Cette courbe a été publiée en 1904 ; c'est à cette courbe que correspondent les figures ci-dessus.

Pour construire cette courbe, il existe deux méthodes. La première méthode consiste à remplacer le deuxième tiers d’un côté du triangle par un triangle équilatéral sans base. Nous débutons donc avec un initiateur puis on remplace chaque segment de la figure par le générateur (voir schéma ci-dessus). Une étape de la construction va être appelée "itération", puisque l'on répète la même opération un certain nombre de fois. La courbe de Von Koch est construite le plus souvent de cette manière.

3 côtés 12 côtés 48 côtés 192 côtés

Il peut être également construit d’une autre façon : il suffit de superposer un triangle équilatéral sur le triangle initial, dont les sommets couperont les côtés de ce dernier. Ensuite il ne reste plus qu’à répéter ce processus indéfiniment.

Mais de nombreuses variations existent, en voici un exemple :

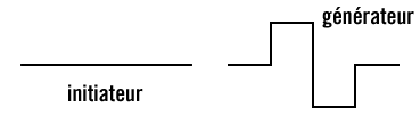
de la courbe de Von Koch

Théoriquement, pour obtenir la fractale, il faudrait faire une infinité d’itérations lors de sa construction mais au bout d’un certain nombre de fois les itérations ne seront plus visibles à cause de leur petite taille.

Il existe une infinité de manière différente de créer des courbes fractales : un autre exemple très connu est le triangle de Sierpinski (ci-dessous). Il est obtenu avec, au départ, un triangle équilatéral noir. Dans ce triangle, nous évidons un triangle équilatéral dont les sommets sont les milieux des arêtes du premier triangle. Ceci nous donne trois triangles noirs équilatéraux plus petits avec lesquels on recommence le même processus.

Les étapes de la construction du triangle de Sierpinsky

Remarque :

Si nous le construisons à partir d'un triangle de Pascal et que nous colorons les nombres pairs en blanc et les nombres impairs en noir, alors le résultat est une approximation du triangle de Sierpinsky. En effet, le triangle de Pascal apparaît comme ci-dessous :

Triangle_pascal Triangle_pascal_colore

Chaque nombre s'obtient par la somme des deux nombres sous lequel il est écrit, hormis pour les 1. Nous pouvons retrouver dans ce triangle un très grand nombre de propriétés : la suite des nombres triangulaires, les puissances de 2 ou la suite de Fibonacci que nous étudierons plus tard. Mais lorsque nous colorons tous les nombres impairs, nous pouvons découvrir le triangle de Sierpinsky !

Voyons maintenant l’ensemble de Mandelbrot, souvent considéré comme « la fractale la plus complexe ».

B) Ensemble de MANDELBROT

Cet ensemble a été inventé en 1981 et. Il représente le symbole des fractales. Il a été découvert par Mandelbrot qui tentait de résoudre le problème suivant : Soit la suite Z_n+1=Z_n²+c avec Z₀=0 et c un nombre complexe quelconque. Mandelbrot s’est posé la question suivante : suivant la valeur de c, quel comportement la suite va-t-elle avoir ? Va-t-elle converger, diverger ou être cyclique ? L’idée est de balayer, à l’aide d’un ordinateur une région de l’espace des complexes. Mandelbrot créa de fascinantes représentations de fractales en gérant des graphes et en utilisant ce que les mathématiciens appellent des « nombres imaginaires ». Il découvrit un ensemble, appelé aujourd’hui l’ensemble de Mandelbrot. Il devient de plus en plus morcelé lorsque l’on zoome sur de petites parties qui, agrandies, révèlent qu’elles se répètent à l’infini. Les mêmes formes de base apparaissent encore et encore, avec d’infinies variations.

L'ensemble de Mandelbrot peut être vu comme un gros bonhomme, avec une tête, un ventre, deux bras, un cou, etc... Cette façon de voir est bien pratique pour se repérer dans le monde imaginaire que représente l'ensemble de Mandelbrot, en utilisant nos connaissances du monde réel. Mais lorsqu'on zoom sur les frontières de Mandelbrot, on s'aperçoit par exemple que la tête principale est elle-même constituée de plusieurs petites têtes (les "oreilles"), qui possèderont à leur tour de nouvelles têtes (qu'on ne pourra plus définir par analogie avec le corps humain) sur leur frontières, et ce, à l'infini. Nous allons parler ici uniquement de têtes, mais nous allons attribuer un numéro à chacune des têtes que nous allons explorer dans notre expérience. Une "tête" est donc une boule ayant pris naissance sur une frontière de l'ensemble de Mandelbrot.

On appelle tête numéro 1 la tête la plus grande de l'ensemble de Mandelbrot, c’est-à-dire la tête principale du "bonhomme" située à gauche. La tête numéro 2 sera la tête située sur le haut de l'ensemble de Mandelbrot (elle correspond à ce qu'on aurait pu appeler "un bras du bonhomme").

L'image suivante montre concrètement les têtes n°1 et n°2 sur l'ensemble de Mandelbrot complet :

La tête n°3 est la plus grosse tête entre les têtes n°2 et n°1

Après avoir défini les deux premières têtes, il est très facile de repérer toutes les autres. Plus une tête est petite, plus nous devrons effectuer de zooms pour aller l'explorer, et plus son numéro sera grand. Nous allons maintenant, en un premier temps repérer les têtes jusqu'à la tête n°8, puis nous les observerons ensuite expérimentalement en analysant certaines particularités.

Chaque tête possède à son sommet une antenne principale, qui se divise en différentes branches. Par exemple, la tête ci-dessous possède 5 branches au total (en comptant l'antenne principale) :

Cette tête possède 5 branches : c'est une tête d'ordre 5

Le nombre total de branches d'une tête (en comptant l'antenne principale comme une branche) est appelé l'ordre de la tête.

La tête n°2 possède 3 branches en tout : c'est une tête d'ordre 3. Parmi toutes les branches d'une tête, il y aura toujours une branche plus courte que toutes les autres. Si on compte les branches dans le sens des aiguilles d'une montre, en comptant l'antenne principale en dernier alors le numéro attribué à la branche la plus courte est appelé le RANG de la tête et celui attribué à l'antenne principale est l'ORDRE de la tête.

On remarque que plus le numéro de la tête augmente, plus la tête possède de branches, et plus le motif représenté par l'ensemble des branches est complexe.

Un zoom est indispensable pour déterminer le numéro de la branche la plus courte, mais aussi pour déterminer le nombre total de branches :

Tête n°7

Zoom sur le haut des branches de la tête n°7

Grâce au zoom effectué entre les branches 13 et 26, on constate sans ambiguïté que la branche la plus courte de la tête n°7 est la branche 21, et que cette tête possède 34 branches au total. On peut donc dire que le rang de la tête n°7 est 21 et que l'ordre de la tête n°7 est 34.

Récapitulons l'ensemble des résultats de ces observations expérimentales dans un tableau

N° de la tête	Rang de la tête	Ordre de la tête
2	2	3
3	3	5
4	5	8
5	8	13
6	13	21
7	21	34

On remarque que le rang et l'ordre des têtes de l'ensemble de Mandelbrot forment deux suites de Fibonacci, c’est-à-dire des suites de nombres où chaque terme est égal à la somme des deux termes précédents. On peut donc en déduire le rang et l'ordre des têtes n°8, n°9, n°10, etc... sans les avoirs observés :

N° de la tête	Rang de la tête	Ordre de la tête
1	1	2
2	2	3
3	3	5
4	5	8
5	8	13
6	13	21
7	21	34
8	34	55

Si on appelle F_n les termes de la suite de Fibonacci avec F₁ le premier terme et F₁=F₂=1, on peut remarquer que le rang de la tête numéro n est égal à F_n+1 et l'ordre de la tête numéro n est égal à F_n+2.

Le rang et l'ordre d'une tête étant deux termes consécutifs de la suite de Fibonacci, nos observations nous permettent maintenant d'affirmer que :

Le rapport entre l'ordre et le rang d'une tête de l'ensemble de Mandelbrot, tend vers le nombre d'or lorsque le numéro de la tête tend vers l'infinie.

Ou encore :

Autrement dit, pour une tête dont le numéro est suffisamment grand, on peut écrire que : Ordre = Rang x nombre d'or

L'ensemble de Mandelbrot complet est donc construit autour du nombre d'or.

Les fractales présentent ainsi de nombreuses propriétés que nous allons vous présenter maintenant.

III. Propriétés fractales

Dans un premier temps, nous verrons l’autosimilarité, puis la dimension fractale et enfin nous étudierons le lien qui relie les fractales et la théorie du chaos (avec la fractale de Feigenbaum).

A) Autosimilarité

L'autosimilarité est le caractère d'un objet dans laquelle on peut trouver des similarités en l'observant à différentes échelles.

Généralement, les structures fractales sont construites suivant un mécanisme d'itération (de répétition) infini et c'est pour cela qu'on retrouve des détails identiques ou similaires à chaque itération. En effet, dans de nombreuses fractales, nous pouvons observer uniquement une similarité des détails, qui ne sont pas toujours strictement identiques au tout. Nous pouvons « zoomer » à l'infini dans une image fractale et il y aura toujours autant de détails. Dans le cas de la courbe de Von Koch les détails sont rigoureusement identiques, c’est donc ici un exemple très simple de cette propriété. C'est pourquoi, lorsque nous regardons une portion de cette figure il est impossible de définir l’échelle à laquelle nous l’observons, ou si nous avons fait un zoom de 10 fois, 100 fois, ou 1 million de fois. Cette propriété montre que les images fractales théoriques ne font apparaître aucune autre figure géométrique ou aucune courbe mathématique : malgré un zoom à l'infini, nous constaterons toujours de nouveaux détails. C'est cet aspect particulier de la notion d'infini qui rend les fractales si fascinantes et qui a contribué à leur popularité.

Exemple d’autosimilarité : ensemble de Mandelbrot

Cet ensemble fractal est impressionnant et les détails que nous y trouvons en zoomant et parcourant l'objet sont spectaculaires.

La mise en abyme (on écrit parfois aussi mise en abîme) est un procédé consistant à incruster une image en elle-même ou, d'une manière générale, à représenter une œuvre dans une œuvre de même type. On y retrouve ici le type d’autosimilarité qui constitue également le principe des fractales. Dans certaines œuvres de théâtre et de cinéma, un comédien joue le rôle d'un comédien qui joue un rôle (procédé appelé communément « théâtre dans le théâtre »). Ce procédé crée un trouble dans la convention narrative : il permet de donner le tournis au lecteur ou à l'auditeur qui rapidement ne sait plus qui parle.

Passons maintenant à une propriété complexe : la dimension fractale.

B) Dimension fractale

La dimension et la longueur sont deux termes qui ne signifient pas la même chose. Rappelons la dimension d’objets courants par des exemples:

· Un point ne se mesure pas : il a pour dimension 0.

· Une ligne droite, une courbe, est mesurée en mètre : elle a pour dimension 1

· Une surface plane comme un quadrilatère ou un disque est mesuré en mètre carré : les surfaces ont pour dimension 2.

Prenons le cas d’un carré. Un carré est un objet de dimension deux car il ne peut être représenté que dans un espace à deux dimensions, c’est-à-dire dans un plan où un point est repéré par deux nombres (abscisse et ordonnée). Cependant, la dimension du carré peut être interprétée d’une autre façon.

Multiplions la longueur de son côté par deux. Nous obtenons la figure ci-dessous.

Or nous remarquons que la surface du carré a été multipliée, elle, par un facteur 4, c’est-à-dire 2² (« deux puissance 2 »). De même, si l’on dilate ce carré par 3, sa surface sera multipliée par 9, soit 3².

Une dilatation par n multiplie la surface de la figure par n². (Dimension 2=> m² => mètre carré)

· Un volume, comme le cube ou la boule, est mesuré en mètre cube : les volumes ont pour dimension 3.

Dans le cas du cube, une multiplication de la longueur du côté (ou une dilatation) par 2 provoque un accroissement du volume par 2³=8.

De façon générale, une dilatation par n multiplie le volume du cube par n³.

Étudions maintenant le flocon de Von Koch. Si l’on dilate le flocon par 3, on obtient un nombre de petits segments 4 fois supérieur (12 segments avant dilatation, 48 segments après dilatation).

On peut donc dire que le flocon a été “multiplié par 4 (car on ne s’intéresse pas à la surface du flocon, mais au nombre de petits segments qui le composent).

$d = \frac{\ln(n)}{\ln(h)}$ Quand la fractale présente la propriété d’autosimilarité, sa dimension fractale peut se calculer comme ce qui suit :

où la fractale de départ est formée de n exemplaires dont la taille a été réduite d'un facteur h (pour homothétie). Malheureusement le logarithme népérien étant une notion de terminale nous ne pouvons pas vous expliquer comment cette formule a été réalisée.

Un côté du flocon de Koch est formé de n = 4 exemplaires de lui-même réduit d'un facteur h = 3. Sa dimension fractale vaut :

$d= \frac{\ln(4)}{\ln(3)} \simeq 1,2618595...$

Le triangle de Sierpinsky est formé de n = 3 exemplaires de lui-même réduit d'un facteur h = 2. Sa dimension fractale vaut :

$d= \frac{\ln(3)}{\ln(2)} \simeq 1,5849625...$

Pour les figures habituelles formées de lignes droites ou courbes de la géométrie classique cette dimension vaut 1, mais la dimension fractale peut prendre des valeurs qui ne sont pas des nombres entiers : elle est supérieure à 1 et inférieure ou égale à 2, mais la dimension 2 ne peut pas être dépassée car c'est la dimension euclidienne des surfaces.

C) Fractale et théorie du chaos, (l’effet papillon)

« Un papillon qui bat des ailes au Brésil peut déclencher une tornade au Texas »

Une infime modification des conditions initiales peut entrainer un impact énorme sur les conséquences : on appelle ce phénomène le chaos.

Prenons l’exemple du flipper. La bille propulsée n’aura jamais la même direction. De toutes petites différences dans la position initiale des billes ou dans la force avec laquelle elles sont propulsées se traduiront par des changements importants dans leur trajectoire. De même on a supposé que le battement de l’aile d’un papillon pouvait modifier radicalement l’avenir climatique voire créer un ouragan.

La notion de fractale et la théorie du chaos sont deux concepts provenant de principes très différents mais on peut faire le rapprochement entre les deux. Lors de l’étude d’un objet fractal ou d’un objet chaotique, nous ne pouvons prévoir la valeur, même approchée, d’un point intermédiaire en connaissant deux autres points très proches.

Mandelbrot a imaginé que la forme complexe d’une fractale est peut-être due à des mécanismes simples répétés un très grand nombre de fois et superposés. C’est comme cela qu’il a permis le rapprochement avec une autre théorie innovante émergée à la même époque que celle des fractales : la théorie du chaos. Edward Lorenz, météorologiste de formation, fut l’un des premiers à s’intéresser au phénomène du chaos. D’autres chaoticiens et lui-même ont constaté qu’une simple équation répétée un grand nombre de fois peut générer une suite de nombres sans cycle, imprévisible : nous disposons alors d’un véritable générateur de hasard. C’est comme cela que Lorenz a supposé que le battement d’aile d’un papillon pouvait engendrer des désastres !

Chaos et fractales sont des concepts intriqués. Ainsi, certains pensent aujourd'hui que la totalité des formes de la nature, y compris celles qui paraissent les plus compliquées, les moins symétriques, les plus détaillées, ont pour origine de simples processus chaotiques qui génèrent des formes à propriétés fractales plus ou moins évidentes (pour les mathématiciens, les notions de fractales et de chaos sont toutes deux basées sur des relations de type non linéaires).

Le point commun de toutes ces nouvelles idées, c'est la répétition. Les fractales et le chaos naissent de la répétition.

Précisons enfin que les fractales mathématiques, dans cet univers complexe et incalculable, représentent seulement l'un des aspects de ces lois du hasard, et non la seule forme qu'elles peuvent adopter.

La fractale de FEIGENBAUM:

Mitchell FEIGENBAUM, né en 1944 à Philadelphie (USA), est un mathématicien et physicien qui a étudié la théorie du chaos. Il a découvert durant ses recherches une constante qui porte son nom : S ≈4,669 201 609 102…

Cette première constante que FEIGENBAUM a trouvée en 1975 est le coefficient de contraction horizontale.

Cette constante est très curieuse car on la retrouve dans les phénomènes physiques : dynamique des fluides, électroniques, lasers, acoustique… IL semblerait donc que cette constante joue un rôle important (comme π et e). On trouve même un lien entre l’ensemble de Mandelbrot et le diagramme des bifurcations. Comme on retrouve les nombres obtenus précédemment dans des nombreux phénomènes physiques, des systèmes hydrodynamiques, cela permet de déterminer si ces systèmes sont stables et à quel moment ils peuvent devenir instables.

On peut illustrer la célèbre phrase de LORENZ : « Un battement d’aile de papillon au Brésil peut entraîner une tornade au Texas » par l’exemple suivant :

Prenons k=4 et (U_n) la suite définie par :

U₀=0.1 et U_n+1=4U_n (1-U_n) pour tout entier naturel n,

Et la suite (V_n) définie par :

V₀=0.1+10^-30 et V_n+1=4V_n (1-V_n) pour tout entier naturel n.

On s’attend à un comportement quasi-identique des suites (U_n) et (V_n).

Donc si on représente graphiquement les points (U_n; V_n) ces points devraient êtres très proches de la droite d’équation y=x.

Mais il n’en est rien! On peut le constater sur le graphique suivant (réaliser ave un calculateur travaillant avec 1000 décimaux) :

Les suites ont un comportement chaotique : nous n’avons pas pu prévoir leur représentation graphique. C’est ainsi pour le battement d’aile d’un papillon. Cette théorie est aussi illustrée dans le film « L’effet Papillon » où Evan TREBORN à la faculté de changer son passé. Il va d’abord mettre son don au service de ceux dont les vies ont été brisées, notamment sauver la seule fille qu’il ait jamais aimée. Mais Evan découvre que son don puissant est incontrôlable : lorsqu’il change une moindre chose, même infime, tout change et a des effets catastrophiques sur le présent.

Le diagramme de Feigenbaum

Fractale de FEIGENBAUM

Certains objets fractals ne satisfont pas toutes ces propriétés, tout en étant des modèles fractals étudiés.

Voici un film montrant un zoom sur un fractal (à télécharger et regarder avec le logiciel gratuit VLC):

film

Conclusion :

Nous pouvons conclure que la beauté et la forme des fractales présentent des ruptures et des continuités. En effet si nous faisons un zoom sur une quelconque partie d’une fractale nous retrouvons toujours la même construction, la même forme mais si sa longueur croit indéfiniment, sa surface, elle, est stabilisée à un moment donné (son aire est limité) la surface d’une fractale peut se contenir dans un carré. Ainsi les fractales se distinguent des autres domaines scientifiques. Elles font en quelque sorte un pont entre l’art (la beauté), un moyen d’expression et de création fondé sur les émotions et l’imaginaire, et la science, une discipline théorique, expérimentale et cohérente. Les fractales sont devenues, depuis quelques années, un domaine d'étude en pleine expansion. C'est un genre de figure que l'on retrouve aussi bien en mathématiques, qu'en biologie, en géographie, en physique, en géologie et même en art ou au cinéma, où elles servent à créer des paysages étranges. Dans la littérature, le procédé d’autosimilarité (mise en abyme) entraîne souvent une sensation de vertige. Les fractales ont permis de montrer une autre vision du monde. Cependant elles restent un domaine scientifique où les chercheurs ont encore beaucoup de choses à découvrir, à comprendre et à apprendre.

Lexique :

Fractal ou fractale : Se dit de figures mathématiques dont la détermination repose sur le principe de la fragmentation. Partie des mathématiques qui étudient et déterminent ces figures.

Ce mot existe au genre féminin et masculin.

Géométrie fractale : La géométrie est la partie des mathématiques qui étudie les figures de dimension fractale.

Bibliographie :

http://fractales.sectionpc.info/tpe%20fractales.pdf

http://www.futura-sciences.com/fr/doc/t/mathematiques/d/les-fractales_234/c3/221/p1/

http://fractals.iut.u-bordeaux1.fr/jpl/dimension.html

http://icosaweb.ac-reunion.fr/Algorithmes/Geometrie/Fractales/TPEFractalesAvril2003B.pdf

http://www.jutier.net/contenu/fractale.htm

http://www.supinfo-projects.com/fr/2005/fractales_theorieduchaos_2005/

http://www2.cnrs.fr/presse/journal/1709.htm

http://eljjdx.canalblog.com/archives/2008/08/03/10122451.html

http://pharouest.ac-rennes.fr/e290062K/projets/fractales/applications/applications.htm